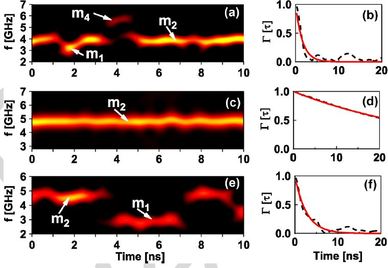
Spin torque oscillators (STOs) often exhibit multiple modes, leading to complex behavior. One example is mode hopping between different eigenmodes of a magnetic tunnel junction (MTJ) STO. This mode hopping is a strong function of current and angle between the magnetization in the free and fixed layers, and away from anti-parallel configuration, mode hopping can be the dominant decoherence process. Another example is the linewidth of a nanocontact STO that can be a complex non-monotonic function of temperature in regions where two or more modes are excited by the oscillators. These phenomena require a generalization of the single-mode nonlinear STO theory to include mode coupling. We derive equations describing the slow time evolution of the coupled system and show they describe a dynamically driven system, similar to other systems that exhibit mode hopping in the presence of thermal fluctuations. In our description, mode coupling also leads to additional coupling between power and phase fluctuations, which can in certain limited cases lead to longer relaxation times for power fluctuations, and consequently to larger linewidths through the nonlinear frequency shift.

O. Heinonen, P. Muduli, E. Iacocca, and Johan Åkerman, Decoherence, Mode Hopping, and Mode Coupling in Spin Torque Oscillators, IEEE Trans. Magn. 49, 4398 (2013).

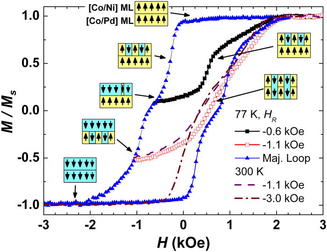We have observed distinct temperature-dependent magnetization reversal modes in a perpendicular (Co/Pd)4/Co/Cu/(Co/Ni)4/Co pseudo-spin-valve, which are correlated with spin-transport properties. At 300 K, magnetization reversal occurs by vertically correlated domains. Below 200 K the hysteresis loop becomes bifurcated due to laterally correlated reversal of the individual stacks. The magnetic configuration change also leads to higher spin disorders and a significant increase in the giant magnetoresistance effect. First order reversal curve measurements reveal that the coupled state can be re-established through field cycling and allow direct determination of the interlayer coupling strength as a function of temperature.

J. E. Davies, D. A. Gilbert, S. M. Mohseni, R. K. Dumas, J. Åkerman, and Kai Liu, APL 103, 022409 (2013).